2019下半年教师资格面试考试初中数学试题及解析4

https://www.hteacher.net 2020-01-05 11:27 中国教师资格网 [您的教师考试网]

1.题目：九年级《蒙古包圆柱圆锥侧面积》片段教学

2.内容：

3.基本要求：

(1)试讲约10分钟;

(2)有分析、解决问题的过程;

(3)要有讨论环节，

(4)要有适当板书。

【试题解析】

一、创设情境，悬疑导入

问题1：同学能举出生活中见到的圆柱、圆锥吗?我们能计算这些物体的那些量呢?

把问题重点放在侧面积的计算上。

回顾复习：圆柱、圆锥侧面积计算的思路以及公式。

问题2：生活中有这么多的圆柱、圆锥、必然在生活会有关于它们的数学计算，今天，我们一起来走进关于圆柱和圆锥侧面积的应用。引出课题《蒙古包圆柱圆锥侧面积》。

二、合作探究，新课讲授

(一)呈现情境，提出问题

创设蒙古包的情境问题，PPT呈现直观图片。

提出问题1：这个问题的突破口在哪里?

诱导学生思考明确：求出一个蒙古包需要用的毛毡的面积。

问题2：那么，一个蒙古包需要用的毛毡的面积该怎么计算呢?

引导学生小组讨论，思考解决方案

(二)画示意图，明确思路

把实际问题抽象成数学问题。ppt呈现几何直观图。

问题1：我们要求是圆柱和圆柱的那些面积呢?

明确：求圆锥和圆柱的侧面积。不需要求底面积，点出易错点。

问题2：我们已知哪些数学量，会利用哪些公式求解呢?

明确：先要利用圆的面积公式求出底面圆的半径，使用圆柱和圆锥的侧面积公式求一个蒙古包的侧面积。

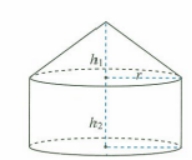
(三)完成解题

问题：那么大家会计算了吗，给大家5分钟时间，大家自主或合作完成，待会请代表上台板演?

学生自主完成解题。

思考：大家求出结果了吗?这个结果就是我们问题所求吗?

点出易错点：容易忘记实际问题是要求20个蒙古包所需要的毛毡面积。

问题：大家可以总结一下在解决实际问题时的一般思路吗?

明确步骤：①审题，明确题意和所求;②把实际问题抽象为数学问题;③思考确定解题思路;④动手实践完善解题过程，发现解决过程的易错点;⑤检验结果，解决问题。

三、巩固应用，内化提高

1.ppt呈现应用题，引导学生以小组为单位解决问题，以小组pk的形式，提高解决问题的热情，对于学生积极表现给予肯定评价。不仅要重结果，更加需要注重学生过程的点播。

(要求学生说明理由。)

四、回顾整理，反思提升

通过今天的实际应用，大家有哪些收获呢，可以说一说，知识上的，方法上的，数学思想上的，等等都行。

引导学生回顾自己的学习过程，畅所欲言，加强反思、提炼及知识的归纳，纳入自己的知识结构。

总结解决问题的一般步骤：①审题，明确题意和所求;②把实际问题抽象为数学问题;③思考确定解题思路;④动手实践完善解题过程，发现解决过程的易错点;⑤检验结果，解决问题。

五、知识拓展，布置作业

1.完成课后习题1题;

2.思考生活中圆柱、圆锥侧面积的应用，下节课一起展示分享。

板书设计：

蒙古包圆柱圆锥侧面积

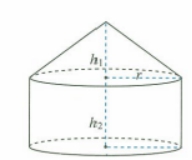
解题思路：①求底面半径r，②求圆柱侧面积，③求圆锥母线长;

④圆锥底面周长;⑤求圆锥侧面积;⑥求出所求。

总结：

①审题，明确题意和所求;

②把实际问题抽象为数学问题;

③思考确定解题思路;

④动手实践完善解题过程，发现解决过程的易错点;

⑤检验结果，解决问题。

责任编辑：郭爽